极点和极线在高中数学中的应用

写在前面的话：

极点和极线是法国数学家笛扎格于1639年在《圆锥曲线论稿》中正式阐述，蕴含了很多圆锥曲线的重要性质。在高中阶段，很多定点定直线问题都以此为背景，所以我们有必要了解一些其定义及性质。

一、从几何角度看极点与极线

几何定义

设 $P$ 是不在圆锥曲线上的一点，过 $P$ 点引两条割线依次交圆锥曲线于四点 $E、F、G、H$ ，连接 $EH、FG$ 交于 $N$ ，连接 $EG、FH$ 交于 $M$ ，则直线 $MN$ 为点 $P$ 对应的极线， $P$ 点叫 $MN$ 的极点。（图1）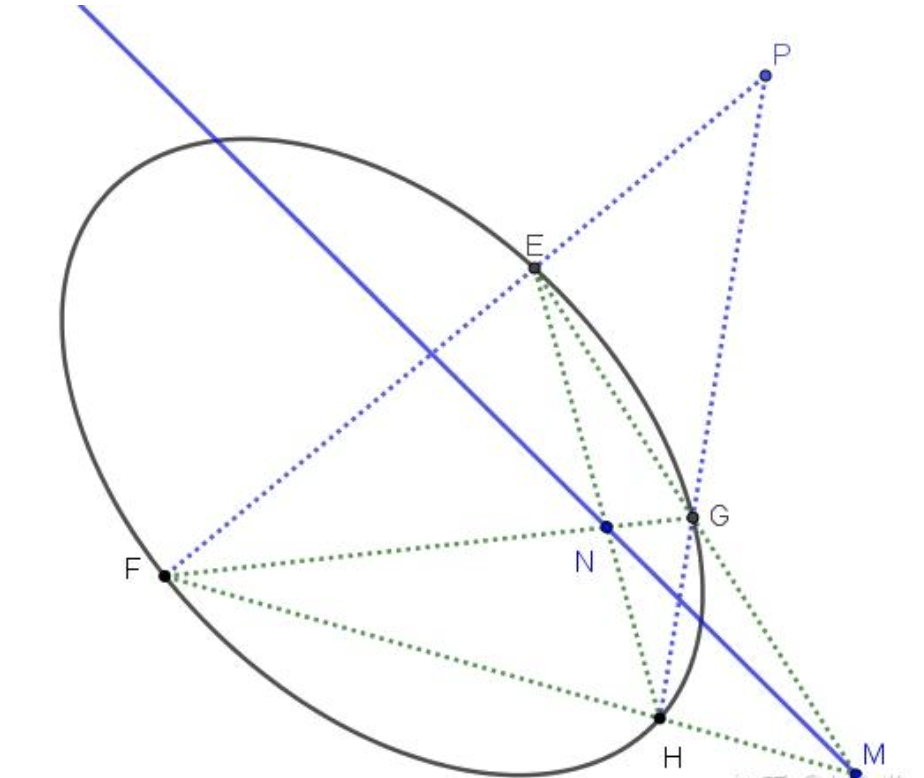

若点 $P$ 为圆锥曲线上的点，则过 $P$ 点的切线即为极线。

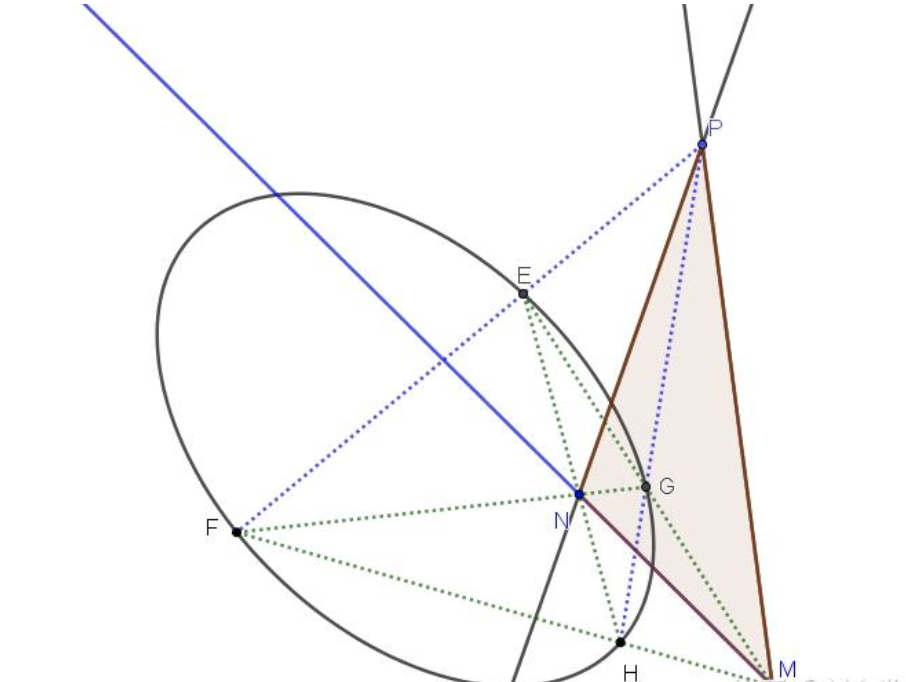
自极三角形

$PM$ 为 $N$ 点对应的极线； $PN$ 为 $M$ 点对应的极线，因而将 $\Delta MNP$ 称为自极三角形。（图2）

极线即为切点弦

设直线 $MN$ 交圆锥曲线于 $A、B$ 两点，则 $PA、PB$ 恰为圆锥曲线的两条切线。（图3）

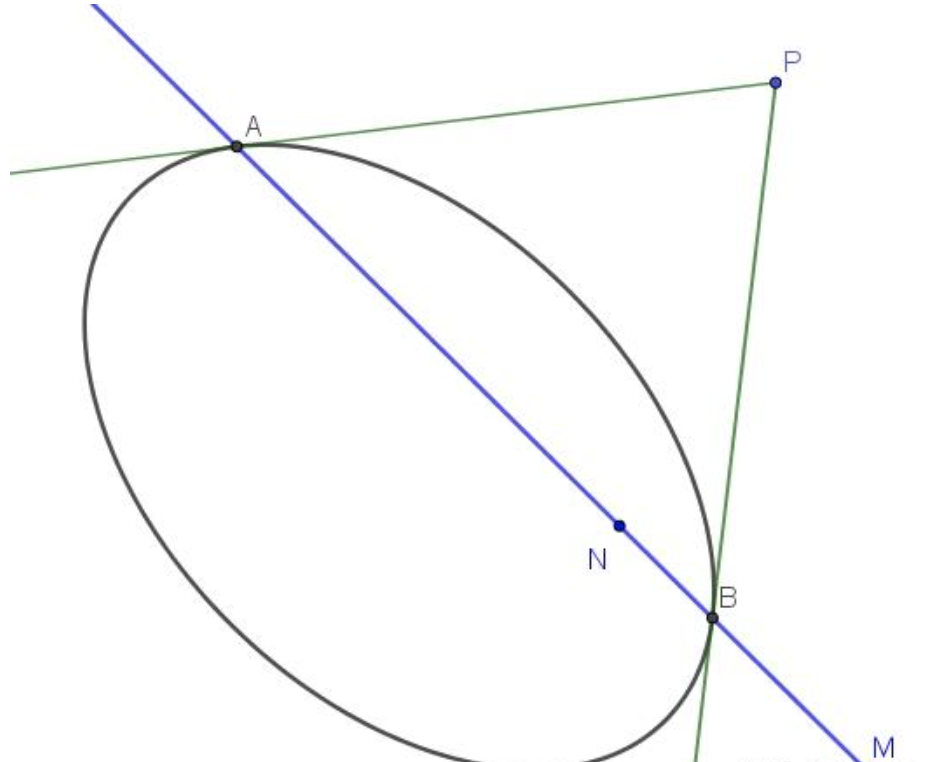
于是我们可以这样理解：过 $P$ 点作圆锥曲线的两条切线，切点为 $A、B$ ，则直线 $AB$ 即为 $P$ 点对应的极线。

GeoGebra中的极线作图工具

在GeoGebra中，有专门的极点极线工具，可以直接作出任一点对应的圆锥曲线的极线：

这里需要说明一下：选定一点和圆锥曲线，利用此工具即可作出该点对应的圆锥曲线的极线；选定一条直线和圆锥曲线，即可作出该直线对于圆锥曲线的径线（与该直线共轭的直径）。

定理1：极线即为切线

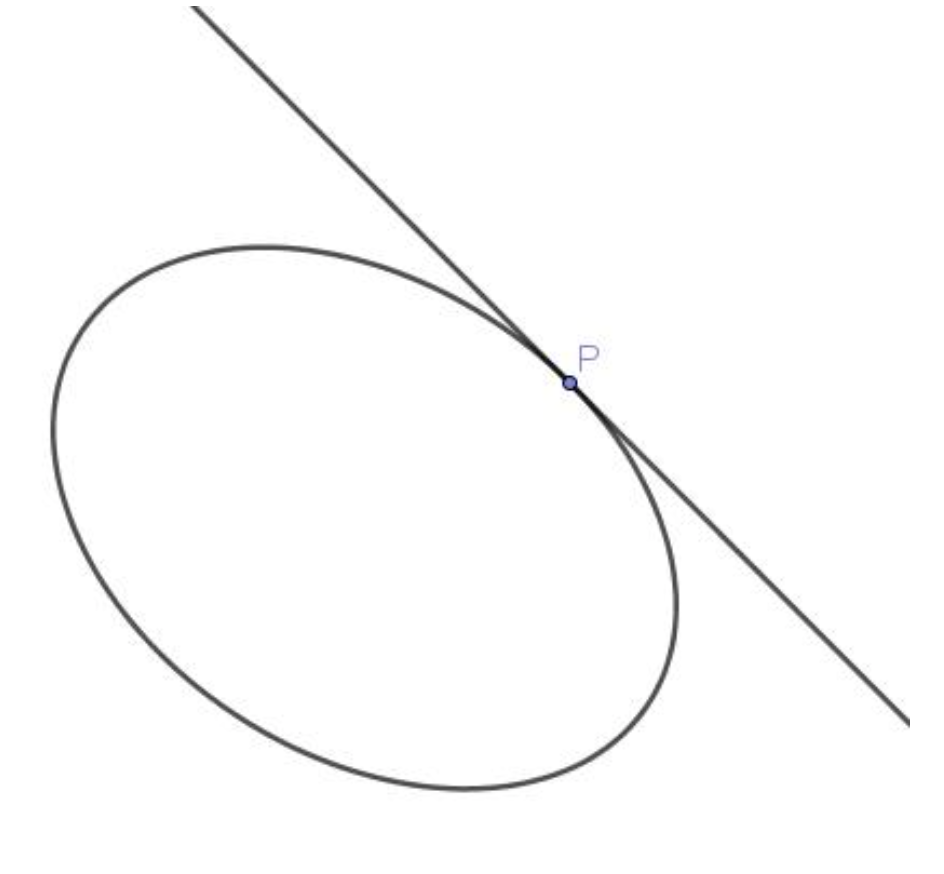
$(1)$ 当 $P$ 点在圆锥曲线 $C$ 上时，则点 $P$ 的极线是圆锥曲线 $C$ 在 $P$ 点处的切线；（图5）

定理2：极线即为切点弦

$(2)$ 当 $P$ 点在圆锥曲线 $C$ 外时，过 $P$ 作圆锥曲线 $C$ 的两条切线，设其切点分别为 $A、B$ ，则点 $P$ 的极线是直线 $AB$ （即切点弦所在的直线）；（图6）

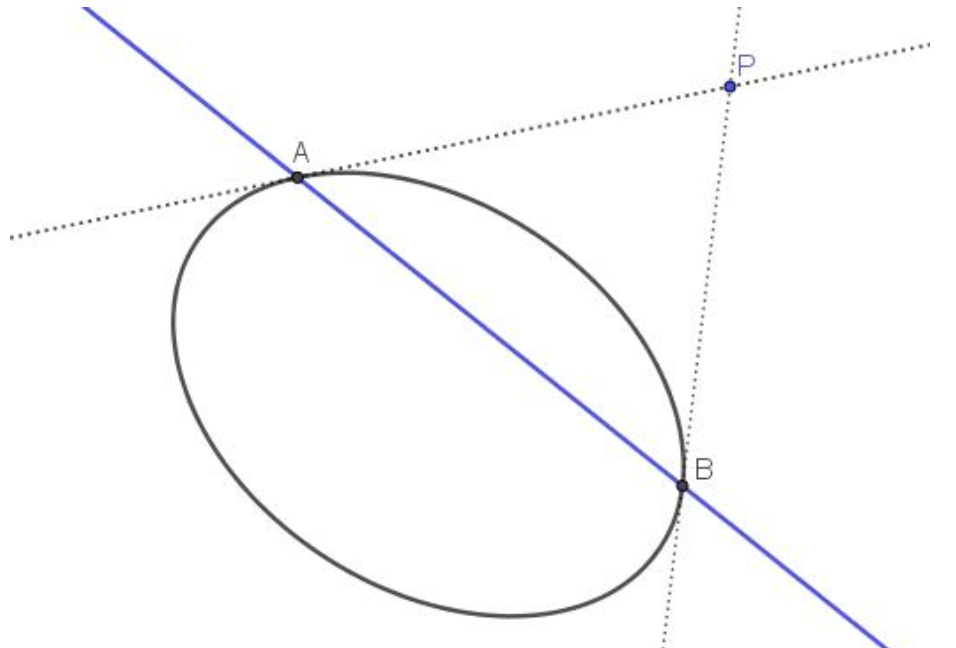
定理3：极线即为两切线交点的轨迹

$(3)$ 当 $P$ 点在圆锥曲线 $C$ 内时，过点 $P$ 任作一割线交 $C$ 于 $A、B$ ，设 $C$ 在 $A、B$ 处的切线交于点 $Q$ ，则点 $P$ 的极线是动点 $Q$ 的轨迹。（图7）

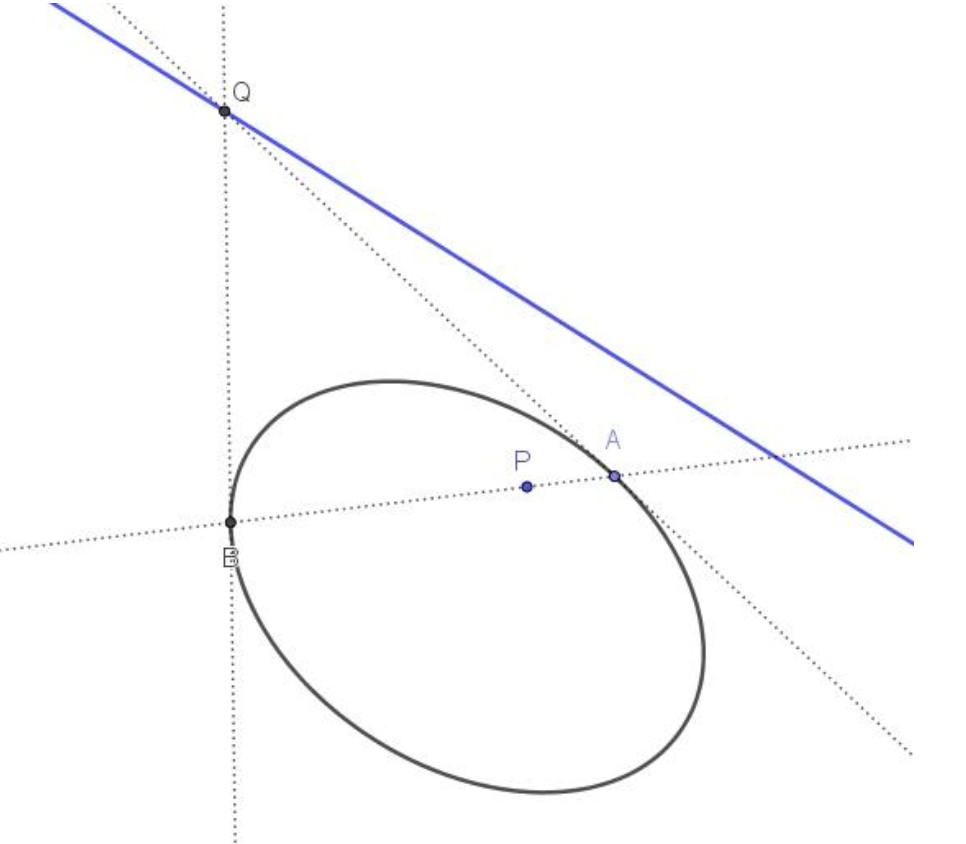
定理4：调和共轭

（如图8）设点 $P$ 关于圆锥曲线 $C$ 的极线为 $l$ ，过点 $P$ 作任一割线交 $C$ 于 $A、B$ ，交 $l$ 于 $Q$ ，则：

$\cfrac{PA}{PB}=\cfrac{AQ}{BQ}\qquad① \\$

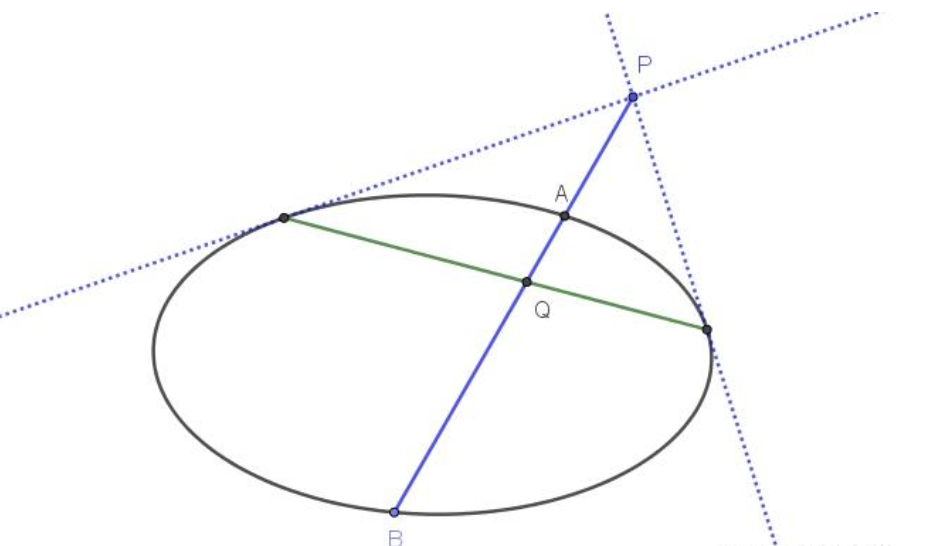
反之：若有 $①$ 成立，则称点 $P、Q$ 调和分割线段 $AB$ ，或称点 $P$ 与 $Q$ 关于 $C$ 调和共轭，或称点 $P(或Q)$ 关于圆锥曲线 $C$ 的调和共轭点为 $Q(或P)$ 。

点 $P$ 关于圆锥曲线 $C$ 的调和共轭点的轨迹是一条直线，这条直线就是点 $P$ 的极线。

推论1：设点 $P$ 关于圆锥曲线 $C$ 的调和共轭点为 $Q$ ，则有 $\cfrac{2}{PQ}=\cfrac{1}{PA}+\cfrac{1}{PB}\quad②$ ；反之若有 $②$ 成立，则点 $P$ 与 $Q$ 关于 $C$ 调和共轭。

可以证明： $①与②$ 是等价的：事实上，由①有：

$\cfrac{AQ}{PA}=\cfrac{BQ}{PB}\Rightarrow\cfrac{PQ-PA}{PA}=\cfrac{PB-PQ}{PB}\Rightarrow\cfrac{PQ}{PA}-1=1-\cfrac{PQ}{PB}\Rightarrow PQ\cdot(\cfrac{1}{PA}+\cfrac{1}{PB})=2\Rightarrow\cfrac{2}{PQ}=\cfrac{1}{PA}+\cfrac{1}{PB}$

特别地，我们还有：

推论2：设点 $P$ 关于有心圆锥曲线 $C$ （设其中心为 $O$ ）的调和共轭点为 $Q$ ， $PQ$ 连线经过圆锥曲线的中心，则有 $OR^2=OP\cdot OQ$ ；反之若有此式成立，则点 $P$ 与 $Q$ 关于 $C$ 调和共轭。（如图9）

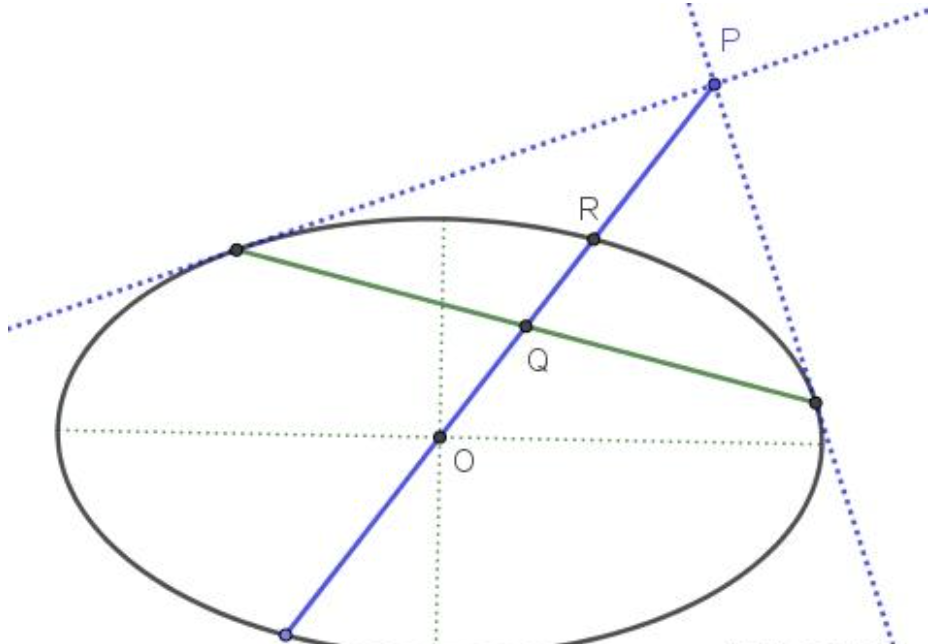
证明：设直线 $PQ$ 与 $C$ 的另一交点为 $R'$ ，则 $\cfrac{PR}{RQ}=\cfrac{PR'}{R'Q}\Rightarrow \cfrac{OP-OR}{OR-OQ}=\cfrac{OP+OR}{OR+OQ}\\$ 化简即得： $OR^2=OP\cdot OQ$

反之由上式可推出： $\cfrac{PR}{RQ}=\cfrac{PR'}{R'Q}$ ，即点 $P$ 与 $Q$ 关于 $C$ 调和共轭。

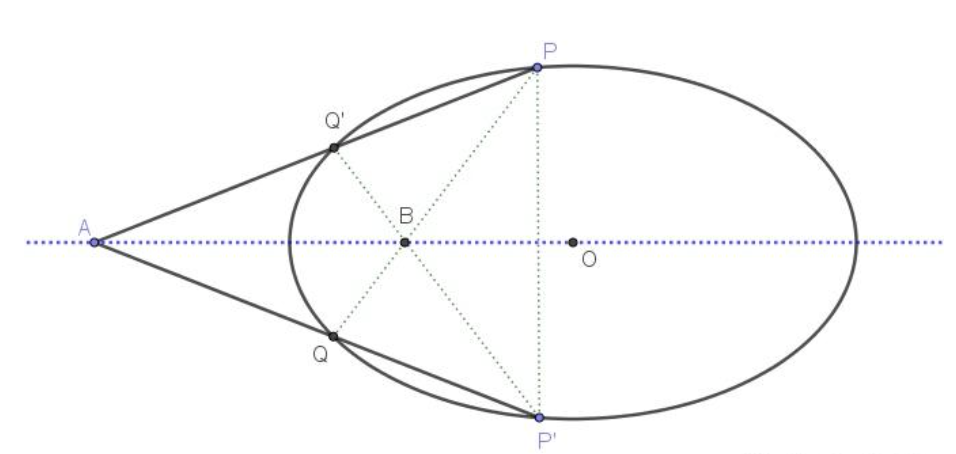
推论3：设 $A、B$ 为关于圆锥曲线 $C$ 的一条对称轴 $l$ 上的两点（不在 $C$ 上），若 $A、B$ 关于 $C$ 调和共轭，过 $B$ 任作 $C$ 的一条割线，交 $C$ 于 $P、Q$ 两点，则 $\angle PAB=\angle QAB$ （图10）

定理5：配极原则

点 $P$ 关于圆锥曲线 $C$ 的极线 $p$ 经过点 $Q$ $\Leftrightarrow$ 点 $Q$ 关于圆锥曲线 $C$ 的极线 $q$ 经过点 $P$ ；

直线 $p$ 关于圆锥曲线 $C$ 的极点 $P$ 在直线 $q$ 上 $\Leftrightarrow$ 直线 $q$ 关于圆锥曲线 $C$ 的极点 $Q$ 在直线 $p$ 上。（图11）

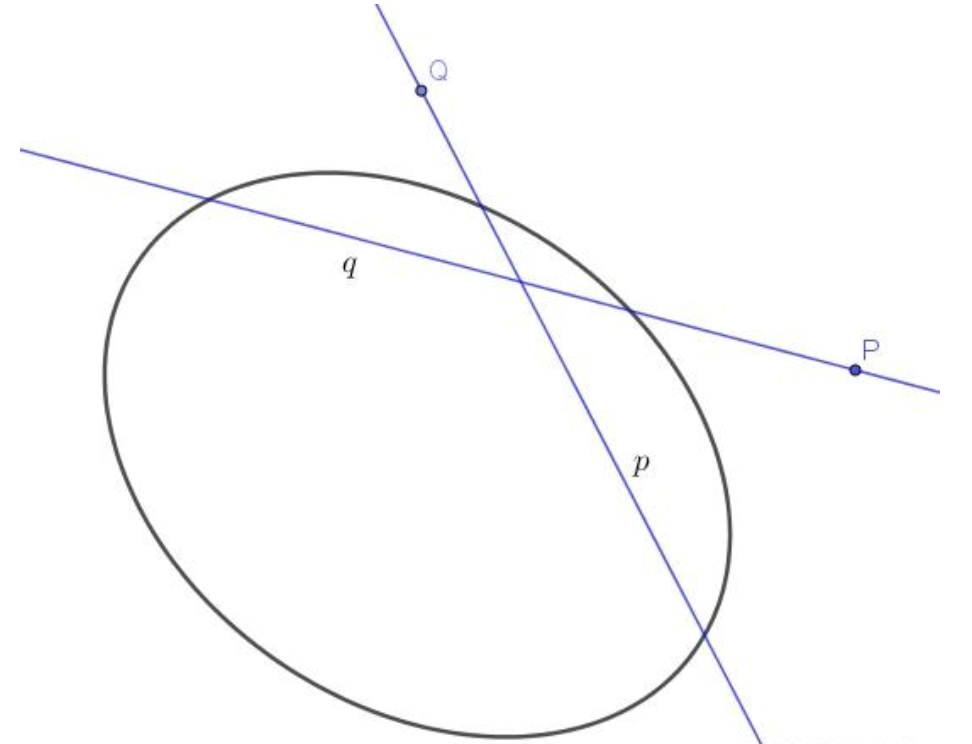
由此可知：共线点的极线必共点；共点线的极点必共线。

二、从代数角度看极点与极线

代数定义

已知圆锥曲线 $C：Ax^2+By^2+2Dx+2Ey+F=0$ ，则称点 $P(x_0,y_0)$ 和直线 $l:Ax_0x+By_0y+D(x+x_0)+E(y+y_0)+F=0$ 是圆锥曲线 $C$ 的一对极点和极线。

事实上，在圆锥曲线方程中，以 $x_0x、y_0y$ 分别替换 $x^2、y^2$ ，以 $\cfrac{x+x_0}{2}、\cfrac{y+y_0}{2}$ 分别替换 $x、y$ ，即可得到 $P(x_0,y_0)$ 的极线方程。

特别地：

$(1)$ 对于椭圆 $\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1$ ，与点 $P(x_0,y_0)$ 对应的极线方程为 $\cfrac{x_0x}{a^2}+\cfrac{y_0y}{b^2}=1$ ;

$(2)$ 对于双曲线 $\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1$ ，与点 $P(x_0,y_0)$ 对应的极线方程为 $\cfrac{x_0x}{a^2}-\cfrac{y_0y}{b^2}=1$ ;

$(3)$ 对于抛物线 $y^2=2px$ ，与点 $P(x_0,y_0)$ 对应的极线方程为 $y_0y=p(x+x_0)$ ;

$(4)$ 如果圆锥曲线是椭圆 $\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1$，当 $P(x_0,y_0)$ 为其焦点 $F(c,0)$ 时，极线恰为椭圆的准线；如果圆锥曲线是双曲线 $\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1$，当 $P(x_0,y_0)$ 为其焦点 $F(c,0)$ 时，极线恰为双曲线的准线；如果圆锥曲线是抛物线 $y^2=2px$ ，当 $P(x_0,y_0)$ 为其焦点 $F(\cfrac{p}{2},0)$ 时，极线恰为抛物线的准线。

三、应用举例

例1、（2021新高考Ⅱ卷）

已知直线 $l:ax+by-r^2=0$ 与圆 $C：x^2+y^2=r^2$ ，点 $A(a,b)$ ,则下列说法正确的是 $(\qquad\quad)$
$A.$ 若点 $A$ 在圆 $C$ 上，则直线 $l$ 与圆相切
$B.$ 若点 $A$ 在圆 $C$ 内，则直线 $l$ 与圆相离
$C.$ 若点 $A$ 在圆 $C$ 外，则直线 $l$ 与圆相离
$D.$ 若点 $A$ 在直线 $l$ 上，则直线 $l$ 与圆 $C$ 相切

略解：由已知，显然直线 $l$ 是点 $A$ 对应的圆 $C$ 的极线，依定义可知答案为 $ABD$ .

例2、（2020年全国高考Ⅰ卷）

已知 $A、B$ 分别为椭圆 $E：\cfrac{x^2}{a^2}+y^2=1(a>1)$ 的左、右项点， $G$ 为 $E$ 的上顶点， $\overrightarrow{AG}\cdot\overrightarrow{GB}=8$ ， $P$ 为直线 $x=6$ 上的动点， $PA$ 与 $E$ 的另一交点为 $C$ ， $PB$ 与 $E$ 的另一交点为 $D$ .
$(1)$ 求 $E$ 的方程；
$(2)$ 证明：直线 $CD$ 过定点。

略解： $(1)$ 依题意： $A(-a,0)，B(a,0)，G(0,1)$

所以 $\overrightarrow{AG}\cdot\overrightarrow{GB}=a^2-1=8$ ，解得 $a=3$ ，于是椭圆 $E$ 的方程为： $\cfrac{x^2}{9}+y^2=1$

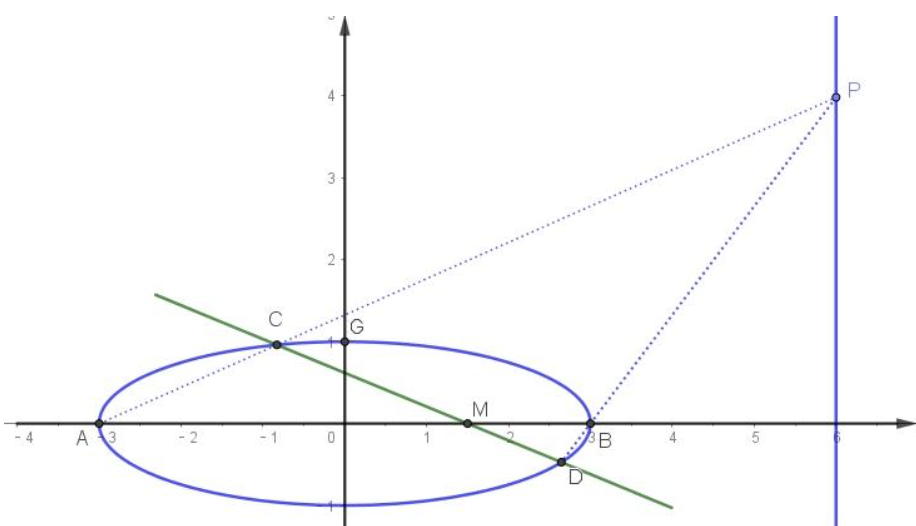
$(2)$ 如图12，由极点极线的定义可知，椭圆方程 $\cfrac{x^2}{9}+y^2=1$ ，以弦 $AB$ 与 $CD$ 交点 $M(x_0,0)$ 为极点， $AC$ 与 $BD$ 的交点一定在极线 $\cfrac{x_0x}{9}+y_0y=1$ 上，即 $\cfrac{x_0x}{9}+y_0y=1$ 与 $x=6$ 为同一条直线，由此可推出 $x_0=\cfrac{3}{2}$ ，即 $CD$ 恒过 $(\cfrac{3}{2},0)$ .

例3、设椭圆 $C：\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 (a>b>0)$ 过点 $M(\sqrt{2},1)$ ，且左焦点为 $F_1(-\sqrt{2},0)$ .
$(1)$ 求椭圆 $C$ 的方程；
$(2)$ 当过点 $P(4,1)$ 的动直线 $l$ 与椭圆交于两个不同的点 $A、B$ 时，在线段 $AB$ 上取点 $Q$ ，满足 $|\overrightarrow{AP}|\cdot|\overrightarrow{QB}|=|\overrightarrow{AQ}|\cdot |\overrightarrow{PB}|$ ，证明点 $Q$ 总在某直线上.

略解：$(1)$ 依题意： $\begin{cases}c^2=2 \\\cfrac{2}{a^2} +\cfrac{1}{b^2} =1 \\c^2=a^2-b^2 \end{cases}$

解得 $a^2=4，b^2=2$ ,所以椭圆 $C$ 的方程为 $\cfrac{x^2}{4}+\cfrac{y^2}{2}=1$

$(2)$ 如图13：

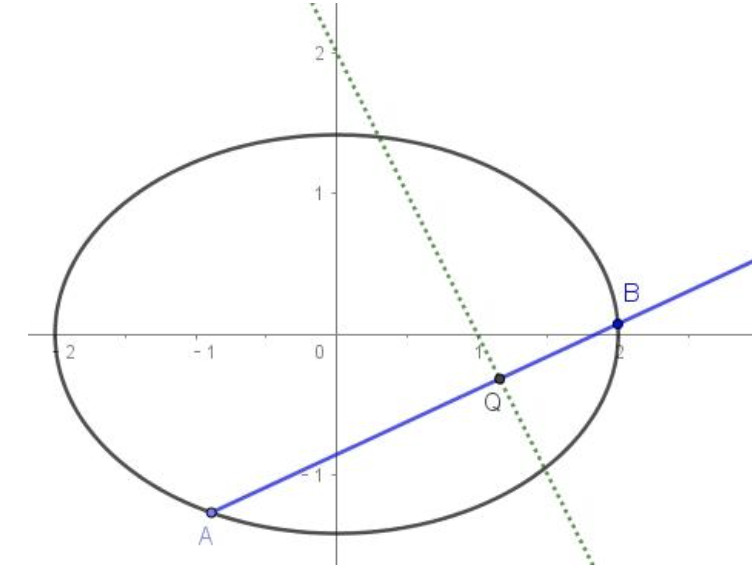
由已知 $|\overrightarrow{AP}|\cdot|\overrightarrow{QB}|=|\overrightarrow{AQ}|\cdot |\overrightarrow{PB}|$ ，可得 $\cfrac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}=\cfrac{|\overrightarrow{AQ}|}{|\overrightarrow{BQ}|}$ ，说明点 $P、Q$ 关于圆锥曲线 $C$ 调和共轭，

即点 $Q$ 的轨迹就是点 $P$ 对应的极线： $\cfrac{4\cdot x}{4}+\cfrac{1\cdot y }{2}=1$，化简得 $2x+y-2=0$

故点 $Q$ 总在定直线 $2x+y-2=0$ 上.

例4、（2022年高考全国乙卷数学（文）21、理20题）

已知椭圆 $E$ 的中心在坐标原点，对称轴为 $x$ 轴、 $y$ 轴，且过 $A(0,-2)$ 、 $B(\cfrac{3}{2},-1)$ 两点，
$(1)$ 求 $E$ 的方程；
$(2)$ 设过点 $P(1,-2)$ 的直线交 $E$ 于 $M、N$ 两点，过 $M$ 且平行于 $x$ 轴的直线与线段 $AB$ 交于 $T$ 点，点 $H$ 满足 $\overline{MT} =\overline{TH}$，证明：直线 $HN$ 过定点。

略解： $(1)$ 设椭圆的方程为 $mx^2+ny^2=1$ ,将 $A$ 、 $B$ 的坐标代入易得 $m=\cfrac{1}{3},n=\cfrac{1}{4}$ ,

于是所求椭圆的方程为： $\cfrac{x^2}{3}+\cfrac{y^2}{4}=1$

$(2)$ 如图14：

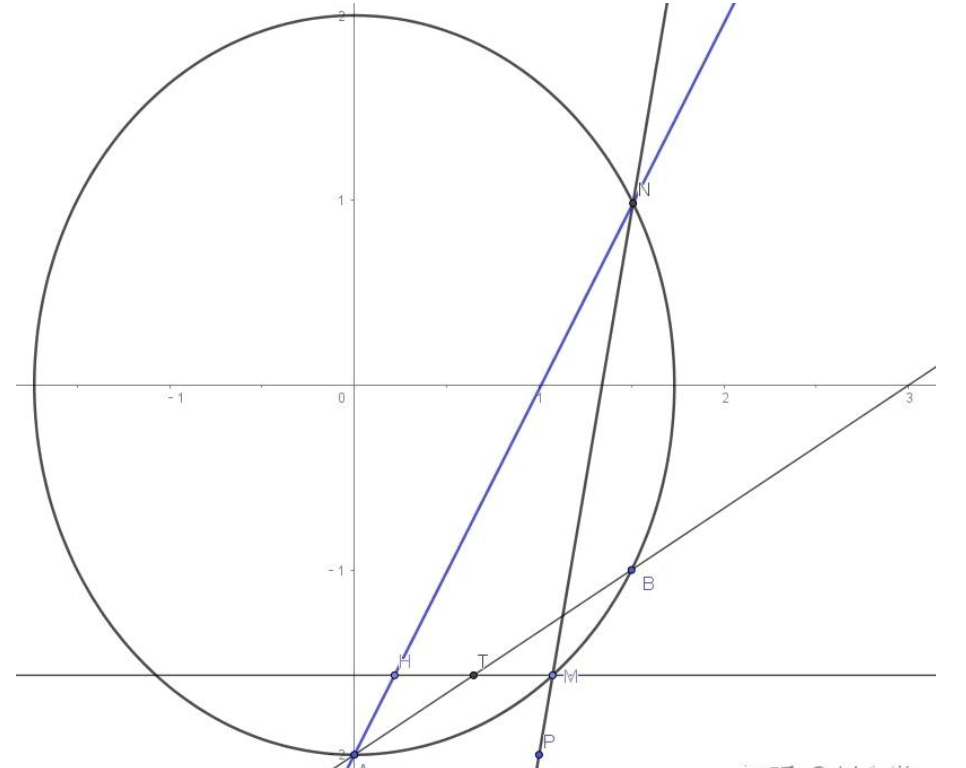
由于$PA、PB$为椭圆切线，于是直线 $AB$ 为 $P$ 对应的极线；

过$M$作$HM\parallel AP$交$AN$于$H$，，$HM\cap AB=T$， 我们证明$T$为$HM$中点.

设$PN\cap AP=Q$，则$(P,Q;M,N)=-1$,

设$AP\cap MH=C$, 则$(M,H;T,C)=-1$,

则$T$为$MH$中点，因此，原题中$HN$恒过点$A(0,-2)$.

下面给出另外一种解法：

直线 $HN$ 过定点 $A$ ，理由如下。

连接 $AN$ 交 $MT$ 于 $H'$ ，只要证 $H=H'$ ，那么 $A,N,H$ 三点共线，即 $HN$ 过定点 $A$ 。

又根据题意， $T$ 为 $MH$ 中点，所以只要证 $T$ 为 $MH'$ 中点。

将坐标原点平移至 $A$ ，即所有图形向上平移2单位（纵坐标+2）。则因为平移不改变线段长度，所以只要证平移后 $MT=TH'$ ，即只要证平移后 $T$ 为 $MH'$ 中点。

此时 $A(0,0),B(\dfrac{3}{2},1)$ ，所以 $AB:x=\dfrac{3}{2}y$ ；椭圆变成 $\dfrac{x^2}{3}+\dfrac{(y-2)^2}{4}=1$ 。

设 $M(x_1,y_1),T(\dfrac{3}{2}y_1,y_1),y_1\in(0,1),N(x_2,y_2),y_2\ne0$ ，则 $AN:x=\dfrac{x_2}{y_2}y$ 。

令 $y=y_1$ 解得 $H'(\dfrac{x_2}{y_2}y_1,y_1)$ ，根据中点坐标公式，只要证 $x_1+\dfrac{x_2}{y_2}y_1=3y_1$ ，即 $\dfrac{x_1}{y_1}+\dfrac{x_2}{y_2}=3$ 。

※平移不改变斜率，上面这个待证式子恰好就是 $\dfrac{2}{k_{AB}}=\dfrac{1}{k_{AM}}+\dfrac{1}{k_{AN}}$ 。

显然 $MN$ 不经过原点 $A$ ，所以设 $MN:mx+ny=12$ 。联立椭圆得 $4x^2-mxy+(3-n)y^2=0$ 。

方程的解为 $M,N$ 坐标，因为 $y_1\in (0,1),y_2\ne0$ ，两边除以 $y^2$ 得 $4(\dfrac{x}{y})^2-m\dfrac{x}{y}+(3-n)=0$ 。

韦达定理得 $\dfrac{x_1}{y_1}+\dfrac{x_2}{y_2}=\dfrac{m}{4}$ 。

注意到 $MN$ 经过 $P(1,0)$ ，代入 $MN$ 方程得 $m=12$ ，所以 $\dfrac{x_1}{y_1}+\dfrac{x_2}{y_2}=3$ 得证。

例 $5、$ 如图：已知抛物线 $C:y^2=2px(p>0)$ ,过直线 $l：y=x+2$ 上点 $P$ 作抛物线 $C$ 的切线 $PA、PB$ ，其中 $A、B$ 为切点( $A$ 在第一象限)，点 $D$ 是 $AB$ 的中点，连接 $PD$ 交抛物线于 $E$ ，已知直线 $AB$ 过定点 $(2,1)$ .

$(1)$ 求抛物线的方程；

$(2)$ 若直线 $AB$ 交 $l$ 于点 $G$ ,是否存在点 $P$ ，使 $\triangle PAG$ 与 $\triangle PBE$ 面积相等 $？$ 若存在，求点 $P$ 的坐标；若不存在，请说明理由。

解： $(1)$ $C：y^2=2x$

$(2)$ 设$A(2y_1^2,2y_1)$，$B(2y_2^2,2y_2)$

则顺势得到：
$D(y_1^2+y_2^2,y_1+y_2)$，$P(2y_1y_2,y_1+y_2)$，$E(\dfrac{(y_1+y_2)^2}{2},y_1+y_2)$
则：$|DE|=\dfrac{(y_1-y_2)^2}{2}$，$|PE|=\dfrac{(y_1-y_2)^2}{2}$

则$S_{\Delta PBE}=\dfrac{1}{2}S_{\Delta PDB}$

若$S_{\Delta PAG}=S_{\Delta PBE}$，则等价于$S_{\Delta APG}=\dfrac{1}{3}S_{\Delta DPG}$

$\begin{aligned}&S_{\Delta APG}=\frac{1}{3}S_{\Delta DPG}\Longrightarrow \\&d_{A-PG}=\frac{1}{3}d_{D-PG}\Longrightarrow \\&x_A-y_A+2=\frac{1}{3}(x_D-y_D+2)\Longrightarrow \\&2y_1^2-2y_1+2=\frac{1}{3}[y_1^2+y_2^2-(y_1+y_2)+2]\end{aligned}$

将①$(y_1+y_2)=2+2y_1y_2$代入等式右边，得到：

$$2y_1^2-2y_1+2=\dfrac{1}{3}(y_1-y_2)^2\tag 1$$

同理由$S_{\Delta BPG}=\frac{5}{3}S_{\Delta DPG}$，得到：

$$2y_2^2-2y_2+2=\frac{5}{3}(y_1-y_2)^2 \tag 2$$

由 $(2)-(1)$ ，化简得到$y_1,y_2$的线性关系：

$\begin{aligned}&2(y_2-y_1)(y_2+y_1-1)=\frac{4}{3}(y_1-y_2)^2\Longrightarrow \\&2(y_2+y_1-1)=\frac{4}{3}(y_2-y_1)\Longrightarrow \\&6y_2+6y_1-6=4y_2-4y_1\Longrightarrow y_2=-5y_1+3\\ \end{aligned}$

代入①：

$\begin{aligned}&2=(y_1+y_2)-2y_1y_2\\&2=(-4y_1+3)-2y_1(-5y_1+3)\\&10y_1^2-10y_1+1=0\\&y_1=\dfrac{10\pm \sqrt{60}}{20}=\dfrac{5\pm \sqrt{15}}{10}\\\end{aligned}$

解一：
当$y_1=\dfrac{5+ \sqrt{15}}{10}$时，$y_2=\dfrac{5-5\sqrt{15}}{10}$，
$P(2y_1y_2,y_1+y_2)=(\dfrac{-10-4\sqrt{15}}{10},\dfrac{10-4\sqrt{15}}{10})$

解二：
当$y_1=\dfrac{5- \sqrt{15}}{10}$时，$y_2=\dfrac{5+5\sqrt{15}}{10}$，$P(2y_1y_2,y_1+y_2)=(\dfrac{-10+8\sqrt{5}}{10},\dfrac{10+4\sqrt{5}}{10})$

答案的复杂，基本规避了暴力运算的可能性，是一道不可多得的好题。

这题关键性的一步线性等式是有推广作用的，原题中，直线$l$是极点$(2,1)$的极线

广义的，抛物线$y^2=2px$，极点$(x_0,y_0)$，极线$yy_0=p(x+x_0)$，经过极点的直线：$x=(y_1+y_2)y-2py_1y_2$，过抛物线于$A(2py_1^2,2py_1)$，$B(2py_2^2,2py_2)$，中点$M(p(y_1^2+y_2^2),p(y_1+y_2))$

极点在直线上：$x_0=(y_1+y_2)y_0-2py_1y_2\Longrightarrow (y_1+y_2)y_0=2py_1y_2+x_0$

$M$到极线的距离：

$\begin{aligned}&\frac{|p(y_1+y_2)\cdot y_0-p\cdot p(y_1^2+y_2^2)-px_0|}{\sqrt{y_0^2+p^2}}\\&=\frac{|p\cdot (2py_1y_2+x_0)-p\cdot p(y_1^2+y_2^2)-px_0|}{\sqrt{y_0^2+p^2}}\\&=\frac{|p^2(y_1-y_2)^2|}{\sqrt{y_0^2+p^2}}\end{aligned}$

对于点 $M$ 、 $A$ 与点 $M$ 、 $B$ 有极线有关系的情况下，两式相减，左式也包含 $y_1-y_2$ ，同上式约取，就能得到$y_1,y_2$的线性关系。

参考资料：

《高考数学大招集锦》湖北教育出版社，王文勇主编